Essentiality checks could help implementers determine with whom they need patent licenses.  However, essentiality checking does a poor job in adjusting for over-declaration in patent counts and will encourage even more spurious declarations.

We await a new policy framework from the European Commission (EC) with its Impact Statement regarding the Fair Reasonable and Non-Discriminatory (FRAND) licensing of Standard Essential Patents (SEPs). The EC is considering instigating checks on patents disclosed—to Standard Setting Organization (SSO) Intellectual Property Rights (IPR) databases as being possibly standard essential— to establish whether they are actually essential to the implementation of standards such as 5G. Objectives for essentiality checking are to:

1. enable prospective licensees to determine with whom they need to be licensed;

2. correct for over-declaration and only count patents deemed essential; and

3. use such figures in FRAND royalty determinations.

If clutches of selected patents are independently and reliably checked to establish that prospective licensors each have at least one patent that would likely be found essential by a court, these results might be used by several or many prospective licensees to determine with whom they need to be licensed. But such checks would be of limited and questionable additional use to existent court determinations. Checks have already been made on some patents for all major licensors and many others in numerous SEP litigation cases over many years. Greater legal certainty is provided in court decisions where many patents have been found standard essential, infringed and not invalid.

This paper focuses on the wider use of essentiality checks and sampling in patent counting. With too many patents to check them all properly, it is hoped that thorough checking of random samples of declared patents will—by extrapolation—also enable accurate SEP counts to be derived. However, essentiality checks do not fix and can only moderate exaggerations in patent counts due to over-declaration. For example, false positive essentiality determinations will exceed correct positive essentiality determinations where true essentiality rates are less than 10% unless at least 90% of determinations are correct. Inadequate checking could imbue many with a false sense of security about precision while encouraging even more over-declaration by others which would further misleadingly inflate their measured patent counts and essentiality rates.

Unfit for purpose

My empirical analysis shows that declared essential patents are too numerous, and bias in checking and random errors in sampling are too great to provide even the modest accuracy expected and that should be required for patent counts to determine FRAND royalties. In-depth and accurate checking on sample sizes of thousands of patents would be required to provide even only low levels of precision in essential patent counts (e.g. a ± 15% margin of error on the estimated patent count at the 95% confidence level)  on patent portfolios and entire landscapes where essentiality rates are low (e.g. 10%) due to over-declarations. This would be prohibitively time-consuming and costly.

Why check patents for essentiality?

The EC appears to remain committed to essentiality checking in its quest to increase “transparency,” as proposed in its new framework for SEPs. Its 2020 intellectual property Action Plan states "The Commission will for instance explore the creation of an independent system of third-party essentiality checks in view of improving legal certainty and reducing litigation costs." However, it is important to ensure information is unbiased and sufficiently precise for whatever purpose this is used.

According to experts “work[ing] on an Impact Assessment Study for the EC” on the topic of SEPs and FRAND licensing “Uncertainty regarding the actual essentiality of declared (potential) SEPs may affect two key dimensions of SEP licensing negotiations: first, whether an implementer needs a license for a particular portfolio of potential SEPs hinges largely on whether that portfolio includes at least one patent that is both valid and essential to a standard that the implementer is using. Second, in some circumstances, the number of patents in a portfolio that are believed to be essential may constitute one guidepost for the determination of a fair, reasonable, and non-discriminatory (FRAND) royalty rate for a license to that portfolio.” 

Patent counting encourages some companies to increasingly over-declare, resulting in ever greater inaccuracies in patent counts. Many declared essential patents are not truly essential or would not be found essential by a court of law in litigation. It is widely believed that some companies significantly “over-declare” and that the true essentiality rates differ widely among SEP owners. It would be also wrong to regard any patent count as a measure of standard-essential patent strength because validity and value also vary enormously among SEPs.

False sense of security

The use of raw counts of declared-essential patents is widely rejected as a way to compare companies’ patent strengths because of over-declaration (i.e. declaring patents excessively above what are or might become essential) and because consensus is that rates of true essentiality vary substantially among patent owners.

Over-declarers will not be deterred by checking and could instead be motivated to declare even more not-essential patents while others are falsely reassured by checking. Essentiality checking does not fix major shortcomings in comparisons of companies’ SEP counts because it only partially reduces disparities arising from over-declarations with the reality of far from perfect checking. Random samples of thousands of patents must be accurately checked to moderate bias and random sampling errors, as discussed below. Improving precision in patent counting is very costly.

More thorough checking—including use of claim charts—should reduce inaccuracy including systemic bias. However, there are too many declared patents to check them all or even one per 

patent family. For example, patents in more than 60,000 families have been declared to 2G, 3G, 4G LTE and 5G standards in the ETSI IPR database.

Sampling to reduce the number of essentiality checks introduces random error in patent counts and essentiality rates. The range of error (i.e. for a given confidence interval) is inversely related to sample size.  And, the lower the true essentiality rate, the larger the range of error as a proportion of the true patent count or true essentiality rate.

In theory, if random samples of declared patents can be accurately checked, unbiased essential patent counts and true essentiality rates can be inferred by extrapolation. Unfortunately, high accuracy in checking is elusive; and variability in patent counts and estimated essentiality rates can be substantial with samples of no more than hundreds of patents if essentiality rates are relatively low. Any royalty-rate derivations from these patent counts will also be subject to wide margins of error.

Inaccurate determinations, prejudicial and systemic biases

A 2017 paper of mine shows huge disparities among companies in the shares of patents found essential to 4G LTE across several different published studies.

Wide variations in shares of found-essential LTE patents among patent-counting studies

	Lowest Estimate	Highest Estimate	Disparity
Huawei	2.9%	23%	8x
LG	0.6%	17%	17x
Nokia	2.3%	54%	23x

Source: WiseHarbor, 2017

Studies produce very disparate results for many reasons; including which patents are included in the patent landscape (e.g. due to timing issues, patent family definitions, applications versus granted patents, focus on user equipment versus network equipment patents), random sampling errors and different essentiality determinations on some of the same patents. The latter occurs because study assessments are typically cursory with less than an hour spent per patent in many cases and because interpreting definitions of essentiality and how patent claims read on the descriptions in technical specifications is a rather subjective matters of opinion. Assessors can be prejudicially biased in favour of study sponsors.

However, significant differences among assessments occur even when assessors are batting for the same team and claim to be coordinating. As a testifying expert witness for Ericsson in TCL. v. Ericsson I was able to compare individual determinations on the same patents and observe that two different TCL experts agreed in only 73% of their essentiality determinations where they both assessed the very same patents. That is not as good as it might seem. It is a mathematical truth that if one of 

them had judged essentiality by the mere flip of a coin (i.e. heads= essential and tails=not-essential, or vice versa) they would be expected to agree with each other in 50% of their determinations.

In my September 2021 seminal paper on non-prejudicial bias and sampling errors in essentiality checking, I also identified what I called “statistical bias.” I also call this “systemic bias” because it is an adverse artefact rather than by design. This bias occurs due to impartial but imperfect essentiality determinations that tend to skew results towards a 50% essentiality rate. On the assumption that true essentiality rates are below 50%, this means that results of essentiality checks tend to be inflated (i.e. appear higher than they really are).

Assessment errors do not “net off” to produce unbiased total essential patent counts. Significantly, averaging results among studies cannot eliminate this bias because all studies are subject to the same bias—although to different extents—depending on the determination inaccuracy of each study. Most studies tend to significantly over-estimate essentiality rates.

The systemic bias arises where assessors are as likely to incorrectly identify an essential patent as they are to incorrectly identify a not-essential patent. This can be is illustrated with an example depicted by a probability tree. In this, with a hypothetical accuracy rate of 75% in essentiality checking, a hypothetical true essentiality rate of 30% inflates to a found essentiality rate of 40%.

Systemic bias with imperfect essentiality determinations 1
(Hypothetical essentiality rate. Hypothetical false positive rate = hypothetical false negative rate)

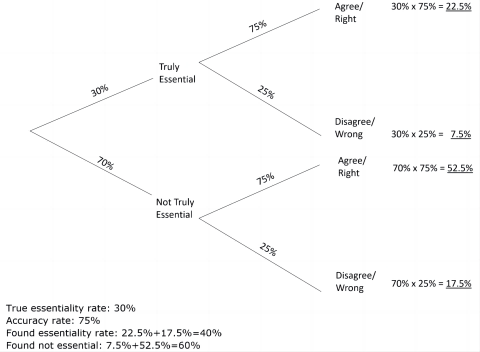
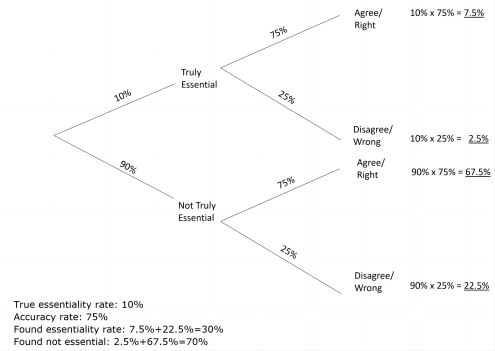
This bias is because the lower the true essentiality rate, the greater the ratio of false positive to correct positive determinations, and the lower the ratio of false negative to correct negative determinations. In comparison to the first probability tree, the second probability tree shows increased bias with a lower hypothetical true essentiality rate of 10% being inflated to a found essentiality rate of 30%.

Systemic bias with imperfect essentiality determinations 2
(Hypothetical essentiality rate. Hypothetical false positive rate = hypothetical false negative rate)

Empirical results show that bias is actually even worse because assessors are rather more likely to incorrectly identify essential patents than they are to incorrectly identify not-essential patents. Analysis on 109 ETSI/3GPP 3G and 4G LTE declared-essential patents in the 2020 EC Pilot Study and in a subsequent 2022 academic paper considered one set of assessments by patent pools to be the reference point for which patents were regarded truly essential and which were not. Many hours were spent checking each patent and in some cases claim charts were used. The two reports’ authors found 74% accuracy overall and 83% (84%) accuracy where claim charts were also used in the secondary assessment. The 2022 publication revealed that “the share of false negatives is [a lot] smaller than the share of false positives (17% vs. 38%).” On that basis, the bias—where true essentiality rates are below 50%—is even more pronounced than in my hypothetical examples above. In comparison to the first probability tree, the third probability tree shows increased bias due to higher rates of false positive than false negative determinations (i.e. independently of essentiality rate). In the latter tree, a hypothetical true essentiality rate of 30% is further inflated to a found essentiality rate of 51.5%.

Systemic bias with imperfect essentiality determinations 3
(Hypothetical essentiality rate. Empirical example of false positive rate >> false negative rate)

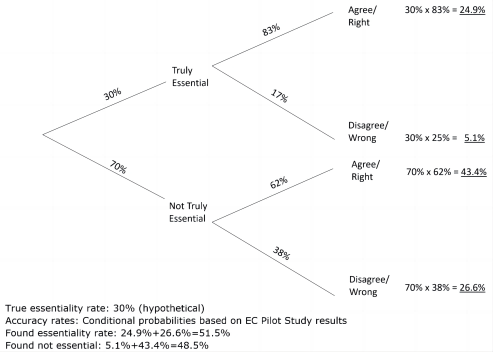
Two factors—true essentiality rates below 50%; and the probability of any individual determination being more likely a false positive than a false negative—compound to yield this strikingly high inflation in found essentiality rates. The latter factor, as measured empirically in the pilot, was not modelled in my September 2021 paper.

Measurement of essentiality assessment accuracy is rather elusive because whether or not patents are truly essential is never established for most declared patents. Only the courts can do that—which will only ever be done for a very small proportion of declared patents.

It is widely believed that thorough essentiality assessments taking many hours and using claim charts, as used by patent pools, in the aforementioned pilot and in David Cooper’s 4G and 5G SEP studies, will produce significantly more accurate determinations than in the cursory checks made in various other patent-counting studies.

Sampling errors

The EC and its advisors favour sampling because, by reducing the number of patents checked, costs can be moderated despite spending more time per patent in preparing claim charts and on essentiality assessment. Total patent counts and essentialist rates can be extrapolated from results of assessments on samples.

Shortcomings I have observed in patent sampling include misapplying the binomial theory, misinterpreting calibrations of standard error and considering sampling error in perfect determinations to be the only sources of inaccuracy.

At least four EC documents on the topic of SEPs cite a 2016 report for the EC by Charles River Associates (CRA) that includes a basic but major mistake in application of fundamental sampling theory with the binomial equation. The claimed level of accuracy “a 95% chance that the actual proportion of truly essential patents in the whole portfolio is between 27% and 33%” would require a sample size considerably more than ten times larger than the mere 30 patents incorrectly claimed to provide “quite a good precision so that the method would not expose patent-holders to any considerable risk of error” with the confidence interval indicated and an undemandingly high essentiality rate of around 30%. One of those EC reports cites the CRA report stating that “A report for the European Commission has also analysed the usefulness of estimates of the share of true SEPs for the purpose of apportionment. It concludes that analysing random samples of declared SEPs would be a reliable and appealing alternative to a thorough assessment of individually declared SEPs.”

I am not aware of any erratum from the CRA and nobody has countered my allegation, which I first made in my September 2021 paper. Baron and Pohlman misleadingly and incorrectly characterise the fundamental and major mathematical mistake in the CRA report as a “disagree[ment between me and CRA] about the correct application of basic statistical theory.”

Metrics and measurements

While the absolute variability remains the same for any given sample size, at lower essentiality rates the variability due to sampling error increases as a proportion of the patent count or essentiality rate. For example, one standard deviation of variability of 5% on a true essentiality rate of 50% is a “10% range” from 45% to 55%.  However, that range is 10%/50%=20% of the true value. The same standard deviation of 5% on a true essentiality rate of only 10% is also a “10% range” (i.e. from 5% to 15%). But that range is 10%/10%=100% of the true value! The discrepancy in these percentage figures and the resulting potential to be confused or mislead about effective accuracy arises because essentiality rates and associated standard deviations are calibrated in percentages. In sampling, measurements for expected outcomes or averages and associated standard deviations are usually calibrated in units, not percentages. For example, if the average number of patents expected to be found essential in sampling is 10 with a standard deviation of 5 patents, that would be a variability range of 10 patents (i.e. from 5 to 15) at the 68% confidence interval level. If one then considered this range as a percentage there would be no doubt this should be as a percentage of the expected value and the variability range would be 10/10=100%.

Such differences in standard errors are important when measuring companies’ relative patent strengths and in deriving or comparing royalty rates. The lower the true essentiality rate, the larger the sample will be required to maintain the precision in such determinations.

Hall of mirrors

My empirical analysis also shows that declared essential patents are too numerous, and bias in checking and random errors in sampling are too great to provide even the modest precision expected and that should be required for patent counts to determine FRAND royalties without very thorough and highly accurate checks on thousands of patents per standard.

The dangers in not recognizing the sources and extent of bias and other errors and in not designing studies with sufficient scale and precision (e.g. for a court setting a royalty rate) is that far from increasing transparency, information provided will be imprecise, distorted and unreliable. Ignoring analytical errors, and mistakenly implying or pretending otherwise is even worse.

Inadequate checking could imbue many with a false sense of security about precision while encouraging even more over-declaration by others which would further misleadingly inflate their measured patent counts and essentiality rates.

This is an abridged and translated version of my full article in English which can be downloaded from SSRN.

Annotation:

¹ This ignores validity and actual infringement in any specific product, which also determine whether licensing is required under patent law and FRAND conditions. These important issues are beyond this paper’s scope.

 ² The essentiality rate is the number of essential patents divided by the number of declared essential patents. Any estimated or found essentiality rate will differ from the true essentiality rate due to inaccuracies.

³ A confidence internal of 95% means that the results would be expected to be in the defined range 95 times if the same population was sampled 100 times. However, no standard for precision in essentiality checking and patent counting has been established. In the absence of even any proposals for this, I provisionally suggested an 85% accuracy (i.e. ±15% “tolerance”) requirement, at least as figure for discussion, in my September 2021 seminal paper on this topic.

⁴ Call for Evidence for an impact statement on Intellectual property – new framework for standard-essential patents, European Commission, 14.02.2022. Communication from the Commission to the European Parliament, the Council and the European Economic and Social Committee and the Committee of the Regions: Making the most of the EU’s innovative potential:  An intellectual property action plan to support the EU’s recovery and resilience;  Brussels 25.11.2020 COM(2020) 760 final. Communication from the Commission to the European Parliament, the Council and the European Economic and Social Committee and the Committee of the Regions: Setting out the EU approach to Standard Essential Patents; Brussels, 29.11.2017 COM(2017) 712 final.

⁵ “An empirical assessment of different policy options to provide greater transparency on the essentiality of declared SEPs;” a paper by Justus Baron and Tim Pohlman presented at the European University Institute Florence Seminar on SEPs, October 2022.

⁶ With in-depth assessments taking many hours and costing around $10,000 per check, as charged by some patent pools, the total cost for 2G/3G/4G/5G could be a huge $600 million, even with only one check for each of 60,000 families. That could be very nice business for lawyers and technical experts, but would be poor value for money and an impractically large task—particularly given that such assessments would not provide legal certainty on essentiality, let alone determine validity or value for any patents.

⁷Do not Count on Accuracy in Third-Party Patent-Essentiality Determinations, by Keith Mallinson, May 2017 (full paper)

⁸ An EC Joint Research Centre report explains the complexities and challenges in formulating patent landscapes: Landscape Study of Potentially Essential Patents Disclosed to ETSI, 2020.

⁹ Pilot Study for Essentiality Assessment of Standard Essential Patents, EC Joint Research Centre, 2020; and Overcoming inefficiencies in patent licensing: A method to assess patent essentiality for technical standards, 2022.

¹⁰ This research revealed nothing about essentiality rates because the sample of patents assessed was not random and is therefore not representative of all patents declared essential to the applicable standard.

¹¹ Evaluating Standards Essential Patents in Mobile Cellular, by David Edward Cooper, les Nouvelles - Journal of the Licensing Executives Society, Volume LIV No. 4, December 2019

Survey of Mobile Cellular 5G Essentiality Rate, by David Edward Cooper, Johanna Dwyer and Alexander Haimovich, les Nouvelles - Journal of the Licensing Executives Society, Volume LVI No. 1, March 2021

¹² Transparency, predictability, and efficiency of SSO-based standardization and SEP licensing, A Report for the European Commission, 2016, by Pierre Régibeau et al., p.61.” Since 2019 Pierre Régibeau is Chief Economist of DG Comp.

¹³σ=(p(1-p)/n)^0.5 where σ= standard deviation of error due to sampling, p=probability=essentiality rate and n= sample size.

¹⁴ Group of Experts on Licensing and Valuation of Standard Essential Patents ‘SEPs Expert Group’, 23/01/2021.  Other EC publications citing that CRA Report include: Call for Evidence for an impact statement. Intellectual property – new framework for standard-essential patents, European Commission, 14.02.2022; Pilot Study for Essentiality Assessment of Standard Essential Patents, Joint Research Centre European Commission, 2020. Communication from the Commission to the European Parliament, the Council and the European Economic and Social Committee: Setting out the EU approach to Standard Essential Patents – COMN (2017) 712 final.

¹⁵ With a normal distribution of results from random samples, 68% of results (i.e. a 68% confidence interval) are expected to be within one standard deviation (either above or below) of the mean result.

About this publication and its author

This article is a shorten version for China IP, the originally unabridged publications was posted to SSRN and published in IP Finance on 16^th November 2022.

Keith Mallinson is founder of WiseHarbor, providing expert commercial consultancy since 2007 to technology and service businesses in wired and wireless telecommunications, media and entertainment serving consumer and professional markets. He is an industry expert and consultant with 25 years of experience and extensive knowledge of the ICT industries and markets, including the patent-rich 2G/3G/4G mobile communications sector. He is often engaged as a testifying expert witness in patent licensing agreement disputes and in other litigation including asset valuations, damages assessments and in antitrust cases. He is also a regular columnist with RCR Wireless and IP Finance – “where money issues meet intellectual property rights.”

The author can be contacted at WiseHarbor. His email address is kmallinson@wiseharbor.com 

© Keith Mallinson (WiseHarbor) 2023.